[논문 리뷰] All in One: Multi-Task Prompting for Graph Neural Network (KDD 2023)

All in One: Multi-Task Prompting for Graph Neural Network

KDD 2023 paper link: https://arxiv.org/pdf/2307.01504.pdf

논문을 읽게 된 계기

최근 LLM의 성능이 매우 좋은데, Graph로 pre-trained model을 fine-tuning하여 downstream task에서의 활용하기 위한 최근 연구가 궁금해서 읽음.

---

💡 3줄 요약

GNN에서의 기존 지도학습이 갖는 데이터 라벨 부족과 과적합 문제를 해결하기 위해 NLP에서 쓰이는 pre-training, fine-tuning 프레임워크를 GNN에 적용하여 pre-training으로 일반적 지식 학습을 수행하여 모델을 초기화하려는 시도가 연구되고 있다.

하지만, downstream task가 될 수 있는 node level, edge, level, graph level task가 각각 너무 상이하여 pre-training 모델의 맥락과 호환되지 않을 경우가 있다.

본 논문에서는, 이를 해결하기 위해 “pretraining and fine-tuning” 구조를 “pre-training, prompting, and fine-tuning”으로 확장한 구조를 제안하며, 많은 실험을 통해 해당 구조의 효과를 증명한다.

---

Terminologies

Pre-training
Pre-training이란 기존에 임의의 값으로 초기화하던 모델의 가중치들을 다른 문제(task)에 학습시킨 가중치들로 초기화하는 방법이다.

Fine-tuning
Fine-tuning은 사전 훈련 이후에 이어지는 단계로, 사전 학습한 모든 가중치와 더불어 downstream task를 위한 최소한의 가중치를 추가해서 모델을 추가로 학습(미세 조정) 하는 방법이다.

Prompting
Prompting 기법은 모델의 동작을 Fine-tuning 과정에서 특정 방향으로 가이드하기 위해 입력 데이터를 재정의하는 기술이다. 이 기법은 입력 데이터에 프롬프트 토큰 또는 지시사항을 추가하여 모델의 행동을 특정 작업 방향으로 이끈다. NLP에서 프롬프트는 일반적으로 입력 텍스트에 부착되는 미리 정의된 구문이나 벡터로, 모델을 특정 작업(예: 질문 답변, 감성 분류)으로 이끄는 역할을 한다.

Introduction

• Challenges in designing graph prompt
  • Language Prompt보다 복잡함
  • downstream task와 pre-trained 모델 간 간극 해결
  • 신뢰할 수 있는 prompt를 학습하기 어려움
    
• Ideas

  • 언어, 그래프 프롬프트 형식 통일(section 3.3).

    1) prompt tokens, 2) token structures 및 3) inserting patterns로 그래프 프롬프트 설계

  • graph-level task로 재정의하는 방법 제안 (section 3.2).

    Original graph에서 유도된 그래프에 의해 node-level 및 edge-level task을 graph-level task로 재정의하는 방법을 제안

  • graph prompt **연구에 meta-learning 기술 도입 (section 3.4).

    Multi-task를 위해 meta-learning 기술을 도입하여 reliable 프롬프트를 학습

3. Multi-task prompting on graphs

3.1. Overview of our framework

목표: 본 논문에서는 원본 그래프에 삽입할 수 있는 프롬프트 그래프를 학습함으로써, 그래프 프리트레이닝 전략과 다양한 다운스트림 작업 간의 격차를 더 좁히고, 사전 지식을 다른 도메인으로 전달하는 어려움을 줄이는 것을 목표로 합니다.

Objective: In this paper, we aim to learn a prompt graph that can be inserted into the original graph, through which we wish to further bridge the gap between a graph pre-training strategy and multiple downstream tasks, and further relieve the difficulties of transferring prior knowledge to different domains.

개요: 이 목표를 달성하기 위해, 우리는 그래프 모델에 대한 새로운 멀티태스크 프롬프트 프레임워크를 제안합니다. 첫째, 우리는 다양한 그래프 작업을 동일한 형식으로 통합하고 이러한 다운스트림 작업들을 그래프 수준 작업으로 재정의 (section 3.2)합니다. 둘째, 통합된 그래프 수준 인스턴스를 사용하여, 학습 가능한 토큰, 내부 구조 및 적응형 삽입 패턴을 가진 새로운 프롬프트 그래프 (section 3.3)를 통해 다중 작업 간의 격차를 더 줄입니다. 셋째, 멀티태스크 설정에서 더 적응적인 그래프 프롬프트를 학습하기 위해 메타러닝 프로세스 (section 3.4)를 구축합니다. 그 다음으로, 주요 구성 요소들에 대해 자세히 설명합니다.

이러한 프레임워크는 그래프 학습 분야에서의 프롬프트 디자인과 다운스트림 작업 일반화에 기여하며, 다른 도메인으로 사전 지식을 전달하는데 도움이 될 수 있습니다

Overview: To achieve our goal, we propose a novel multi-task prompting framework for graph models. First, we unify various graph tasks in the same format and reformulate these downstream tasks as graph-level tasks. Second, with the unified graph-level instances, we further narrow down the gap among multiple tasks by a novel prompt graph with learnable tokens, inner structures, and

adaptive inserting patterns. Third, we build a meta-learning process to learn more adaptive graph prompts for multi-task settings. Next, we elaborate on the main components.

3.2. Reformulating Downstream Tasks

3.2.1. Why Reformulate Downstream Tasks.

NLP에서 “pre-training and fine-tuning” framework가 성공적인 이유는 pre-training task와 downstream task가 공통적인 본질 task를 공유하기 때문이다.

하지만, GNN의 node-level task와 edge-level task는 매우 다른 작업으로, 매우 작은 공통적 본질을 공유한다. → 부정적 전이를 유발할 수 있다.

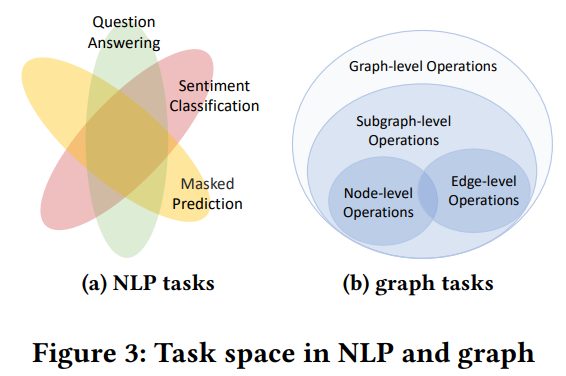
3.2.2 Why Reformulate to the Graph Level.

그래프에서의 잠재적 task space를 재검토하고 Figure 3b에서 보여지는 계층적 관계를 찾았습니다.

node-level (node feature 변경, node 추가/삭제), edge-level (edge 추가/삭제) → 기본적인 graph level 연산으로 다룰 수 있다.

graph-level task가 가장 일반적이며 많은 겹치는 지식 전이에 대한 sub-space를 차지한다.

3.2.3. How to Reformulate Downstream Tasks.

node-level task와 edge-level task를 각각 노드와 엣지에 대한 induced 그래프로 재정의

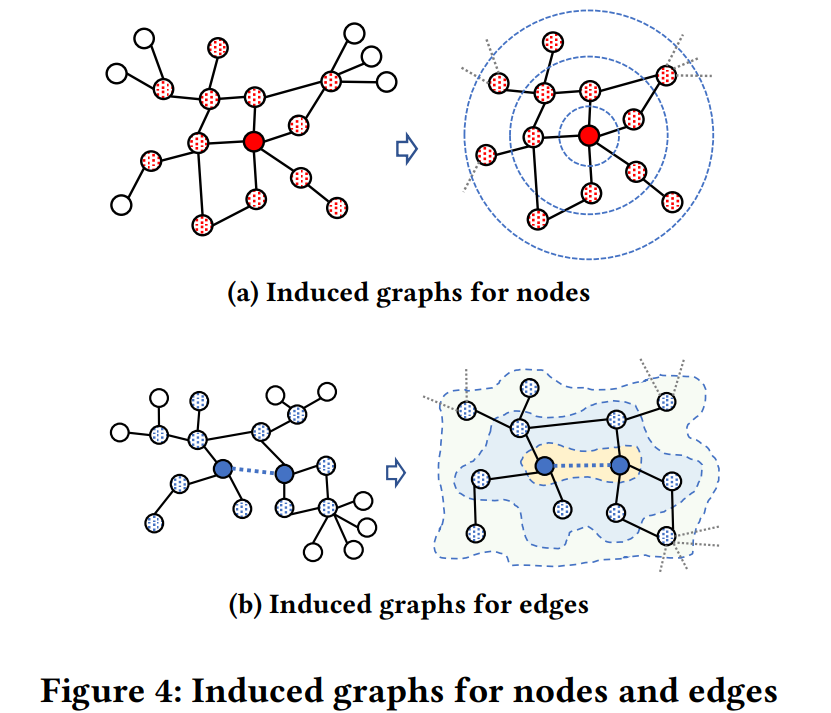
Figure 4a: target node에 대한 induced 그래프는 네트워크에서 해당 노드의 𝜏 거리 이내의 local 영역

Figure 4b: 노드 쌍에 대한 induced 그래프 (노드 쌍은 연결되어 있으면 양의 엣지로 취급되고, 그렇지 않으면 음의 엣지로 취급)

이 하위그래프는 이 노드 쌍을 그들의 𝜏 거리 이내 이웃으로 확장하여 쉽게 구성

edge-level task을 graph label로서 대상 노드 쌍의 엣지 레이블과 함께 재정의

무방향성 그래프의 경우, 𝜏 거리는 𝜏-홉 길이와 같습니다.

가중 그래프의 경우, 𝜏 거리는 최단 경로 거리를 의미하며, 여기서 induced 그래프는 여러 효율적인 알고리즘 [1, 39]을 통해 쉽게 찾을 수 있습니다.

3.3 Prompt Graph Design

3.3.1 Prompting NLP and Graph in One Way.

NLP와 그래프 영역의 프롬프트는 적어도 세 가지 구성 요소를 포함해야 한다는 것을 발견했습니다:

(1) 프롬프트 토큰은 입력 단어/노드 벡터와 동일한 크기의 벡터화된 프롬프트 정보를 포함합니다;

(2) 토큰 구조는 서로 다른 토큰들의 연결을 나타냅니다. NLP 영역에서 프롬프트 토큰(또는 프롬프트 단어)은 하위 문장 또는 구절과 같이 선형적인 관계로 미리 정의되어 있습니다. 반면, 그래프 영역에서는 서로 다른 토큰들의 연결은 비선형적이며 NLP 프롬프트보다 훨씬 복잡합니다;

(3) 삽입 패턴은 프롬프트를 입력 데이터에 어떻게 추가할지를 나타냅니다. NLP 영역에서는 프롬프트가 기본적으로 입력 문장의 앞 또는 뒤에 추가되는 것이 일반적입니다. 그러나 그래프 영역에서는 문장과 같은 명시적인 위치가 없기 때문에 그래프 프롬프트를 추가하는 것이 더 어려워집니다.

3.3.2 Prompt Tokens.

그래프 인스턴스를 G = (V, E)로 표현하고, 여기서 V = {𝑣1, 𝑣2, · · · , 𝑣𝑁 }은 𝑁개의 노드를 포함하는 노드 집합이며, 각 노드는 x𝑖 ∈ R1×𝑑로 표현되는 특징 벡터를 갖습니다. E = {(𝑣𝑖, 𝑣𝑗)|𝑣𝑖, 𝑣𝑗 ∈ V}은 각 엣지가 V 내 노드 쌍을 연결하는 엣지 집합입니다.

우리는 프롬프트 그래프를 G𝑝 = (P, S)로 표현하며, 여기서 P = {𝑝1, 𝑝2, · · · , 𝑝|P|}는 프롬프트 토큰의 집합을 나타내며, |P|는 토큰의 수를 의미합니다. 각 토큰 𝑝𝑖 ∈ P는 크기가 입력 그래프의 노드 특징과 동일한 크기의 토큰 벡터 p𝑖 ∈ R1×𝑑로 표현될 수 있습니다. 실제로, 일반적으로 |P| ≪ 𝑁과 |P| ≪ 𝑑ℎ인데, 이 때 𝑑ℎ는 사전 훈련된 그래프 모델의 은닉층 크기입니다. 이러한 토큰 벡터들을 사용하여 입력 그래프에 𝑗번째 토큰을 더하여 입력 그래프를 재정의할 수 있습니다 (예: xˆ𝑖 = x𝑖 + p𝑗). 그런 다음, 우리는 프롬프트 특징으로 입력 특징을 대체하고, 이를 사전 훈련된 모델에 전달하여 추가적인 처리를 수행합니다.

3.3.3 Token Structures.

S = {(𝑝𝑖, 𝑝𝑗)|𝑝𝑖, 𝑝𝑗 ∈ P}은 토큰 간의 쌍별 관계를 나타내는 토큰 구조를 의미합니다. NLP 프롬프트와 달리, 프롬프트 그래프에서의 토큰 구조는 일반적으로 암시적입니다. 이 문제를 해결하기 위해, 우리는 세 가지 방법을 제안하여 프롬프트 토큰 구조를 설계합니다: (1) 첫 번째 방법은 조정 가능한 매개변수를 학습하는 것입니다: A = |P|−1 ∪ 𝑖=1 𝑗=𝑖+1 {𝑎𝑖𝑗} 이때 𝑎𝑖𝑗는 토큰 𝑝𝑖와 토큰 𝑝𝑗가 연결되어야 할 가능성을 나타내는 조정 가능한 매개변수입니다; (2) 두 번째 방법은 각 프롬프트 토큰 쌍의 내적을 사용하고, 내적 값을 기준으로 쌍을 제거합니다. 이 경우에는 (𝑝𝑖, 𝑝𝑗) ∈ S가 𝜎(p𝑖 · p𝑗) < 𝛿인 경우입니다. 이때 𝜎(·)은 시그모이드 함수이고, 𝛿은 사전 정의된 임계값입니다; (3) 세 번째 방법은 토큰을 독립적으로 취급하고, 그래서 S = ∅가 됩니다.

3.3.4 Inserting Patterns

𝜓는 프롬프트 그래프 G𝑝을 입력 그래프 G에 추가하는 방법을 나타내는 삽입 함수입니다. 이로 인해 조작된 그래프는 G𝑚 = 𝜓 (G, G𝑝)로 표시됩니다. 우리는 삽입 패턴을 프롬프트 토큰과 입력 그래프 노드 간의 내적으로 정의하고, 그런 다음 가중치 값을 사용하여 특정한 연결을 조정하는 방법을 사용합니다. 예를 들어, xˆ𝑖 = x𝑖 + ∑|P|𝑘=1𝑤𝑖𝑘p𝑘와 같이 조작된 노드 xˆ𝑖를 정의할 수 있습니다. 여기서 𝑤𝑖𝑘는 불필요한 연결을 제거하기 위한 가중치 값으로 정의됩니다:

3.4 Multi-task Prompting via Meta Learning

3.4.1 Constructing Meta Prompting Tasks.

supporting data, query data를 지정한다.

graph-level: labeled graph 포함

node-level: 각 node에 대해 induced graph를 생성하여 graph label을 target node label과 호환한다.

edge-level: train, test용 edge induced graph를 각각 생성한다. edge label은 해당 edge의 두 끝점에 따라 결정

3.4.2 Applying Meta-learning to Graph Prompting

𝜃 : prompt parameters, 𝜋∗ : fixed parameters of the pre-trained graph backbone, 𝜙 : tasker’s parameters, 𝑓𝜃,𝜙 |𝜋∗ : pipeline, $ L_{D} (𝑓 ) $ : task loss with pipeline f on data D

매 task $ \tau_i $ 에서 대응하는 parameter는 다음과 같이 갱신된다.

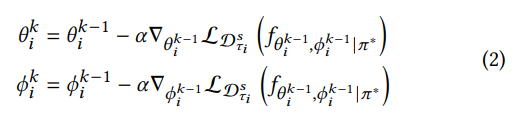
where the initialization is set as: $ \theta_{i}^{0}= \theta, \phi_{i}^{0}= \phi $

목표: meta prompting task를 위해 효과적인 초기값 $(\theta, \phi)$를 얻는 것

방법: 다양한 task의 meta loss를 최소화

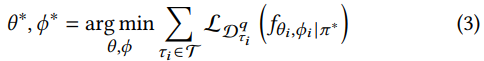
chain rule에 의해 second-order gradient를 이용해 query data를 바탕으로 $\theta(혹은 \phi)$를 갱신한다.

Model-Agnostic Meta-Learning(MAML) framework 사용 - 발전된 First order MAML도 있음.(성능 거의 비슷)

chain rule: ${f(g(x))}’=f’(g(x))\times g’(x)$

First-order gradient: loss function에 대한 파라미터의 변화율을 나타내는 벡터

second-order gradient: 손실 함수의 곡률 정보를 얻을 수 있다.

→ meta loss: task loss를 minimize하기 위한 loss → task loss가 극솟값을 갖는 지점을 second-order gradient를 이용해 찾을 수 있다.

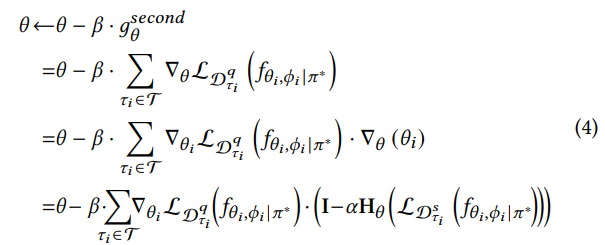
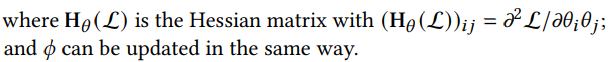
3.4.3 Overall Learning Process.

학습 안정성을 위해 다양한 graph task를 multi-task episode로 구성하고,. node/edge/graph class를 binary classification으로 처리하여 동일한 task head를 공유하도록 한다.

3.5 Why It Works?

3.5.1 Connection to Existing Work.

• GPPT
  • graph prompt 연구
  • edge-prediction을 pre-training의 pretext로 사용하고, node classification을 downstream task로 수행하기 위해 original graph에 추가하는 (prompt) labeled token을 설계함.
• 본 연구와 차이점
  • GPPT is not flexible to manipulate original graphs
  • GPPT is only applicable for node classification
  • GPPT only supports edge prediction task as the pretext but is not compatible with more advanced graph-level pre-training strategies such as GraphCL [36], UGRAPHEMB [2], SimGRACE [35] etc.

3.5.2 Flexibility

프롬프팅의 본질은 입력 데이터를 사전 텍스트와 일치하도록 조작하는 것

data operation의 flexibity는 프롬프팅 성능의 병목이다.

𝑔를 graph-level 변환으로 정의 (such as “changing node features”, “adding or removing edges/subgraphs” etc.) 하여 모든 그래프 G에 대해 적절한 prompt token $p*$을 학습하여 다음과 같은 방정식이 성립할 수 있음을 증명했다. Fang et al. [6]

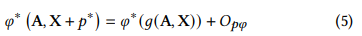
즉, 원본 그래프에 적용될 적절한 토큰을 학습하여 모든 graph manipulation을 모방할 수 있다.

𝑂𝑝𝜑: original graph와 prompted graph의 pre-trained 모델 표현 간의 오차 한계

→모델의 일부 비선형 레이어(unchangeable)와 학습된 프롬프트(changable)의 품질에 영향을 받으며, 발전된 프롬프트 방법으로 더욱 줄일 수 있습니다.

이 논문에서는 독립적인 토큰을 프롬프트 그래프로 확장하여 학습 가능한 내부 구조를 갖는 여러 프롬프트 토큰을 포함하는 방법을 제안합니다.

삽입 함수: 𝜓 (G, G𝑝), G: original graph, G𝑝: prompt graph, G∗𝑝: an optimal prompt graph

효율적인 G∗𝑝 튜닝을 통해 새로운 오차 한계 𝑂∗𝑝𝜑를 더욱 줄일 수 있습니다.

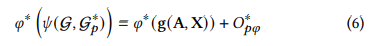
섹션 4.6에서는 효과적인 학습을 통해 𝑂∗𝑝𝜑가 𝑂𝑝𝜑보다 상당히 작을 수 있음을 경험적으로 보여줍니다. 이것은 우리의 방법이 다양한 사전 훈련 전략과 일치하도록 그래프에 더 유연한 변환을 지원한다는 것을 의미합니다.

3.5.3 Efficiency.

we only need to tune the prompt with the pre-trained graph model frozen, making the training process converge faster than traditional transfer tuning.

For the graph features and structures, traditional methods usually need to feed the whole graph into a graph model, which needs huge memory to cache these contents.

실제로 많은 실제 응용 프로그램에서는 전체 노드 중 일부에만 관심을 가지고 있기 때문에 우리의 방법은 필요한 노드가 없으면 적시에 멈출 수 있으며 전체 그래프에서 메시지를 전파할 필요가 없습니다. 이는 대규모 데이터에 특히 도움이 됩니다.

3.5.4 Compatibility.

GPPT(prompt model) vs our model

GPPT보다 더 많은 case에 사용할 수 있다.

Pre-training with fine-tuning vs our model

When transferring the model to different tasks, traditional approaches usually need to additionally tune a task head. In contrast, our method focuses on the input data manipulation and it relies less on the downstream tasks. This means we have a larger tolerance for the task head

5. Conclusion

We propose a novel method to reformulate different-level tasks to unified ones and further design an effective prompt graph with a meta-learning technique.