[논문 리뷰] Universal Prompt Tuning for Graph Neural Network (arXiv preprint)
Universal Prompt Tuning for Graph Neural Network
paper link : https://arxiv.org/pdf/2209.15240.pdf
논문을 읽게 된 계기
All in one: Multi-task prompting for graph neural network (KDD’23) 에서 Graph prompt 학습을 위해 사용하는 수식을 이해하고자 읽음
Main Point
어떤 pre-trained 모델에도 적용 가능한 universal prompt 기반 튜닝 방법인 “Graph Prompt Feature”를 제안한다.
Theorm :모든 그래프 G에 대해 적절한 prompt token $p*$을 학습하여 다음과 같은 방정식이 성립할 수 있음
A, X: Original Graph의 인접행렬과 노드의 특징행렬
𝑔: graph-level 변환(such as “changing node features”, “adding or removing edges/subgraphs” etc.)
𝑂𝑝𝜑: original graph와 prompted graph의 pre-trained 모델 표현 간의 오차 한계
p*: prompt token vector 행렬
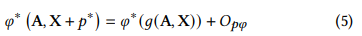from All in one(23’KDD)
Proof
pre-trained GNN 모델에 node feature, adjacency matrix, prompt token feature을 입력으로 넣어서 얻은 embedding과 어떤 prompted graph (modified input graph)를 입력으로 넣어서 얻은 embedding이 같도록 하는 graph prompt feature $\hat{p}$가 존재한다고 가정한다.
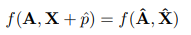
이 때 node level로 hidden layer를 얻는 식을 작성하면 다음과 같다.
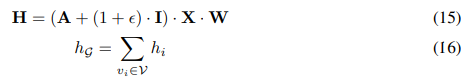
W: 선형변환행렬
The parameters ϵ and W have been pre-trained in advance and remain fixed during downstream adaptation.
We define the graph level transformation g : G → G, which satisfies $ (\hat{A} , \hat{X} ) = g(A, X) $. Consequently, Theorem 1 is equivalent to Proposition 1.
Proposition 1. Given a pre-trained GNN model f, an input graph G : (A, X), for any graph-level transformation g : G → G, there exists a GPF extra feature vector $ \hat{p} $that satisfies:
